graph shortest path - 최단 경로 다익스트라 알고리즘 python
다익스트라 알고리즘
하나의 정점(node) A에서 다른 정점 B까지 최단 경로를 구한다. 이 때 간선들은 양의 weight를 가져야 한다.
시작하는 A를 제외하고는 나머지 node는 미방문으로 초기화하고, 연결되지 않은 값은 inf(무한대)로 표시한다.

시작하는 node에서부터 연결된 노드들의 edge 값을 확인한다. edge 값 중에서 가장 짧은 edge를 선택하여 node의 값을 업데이트 합니다.
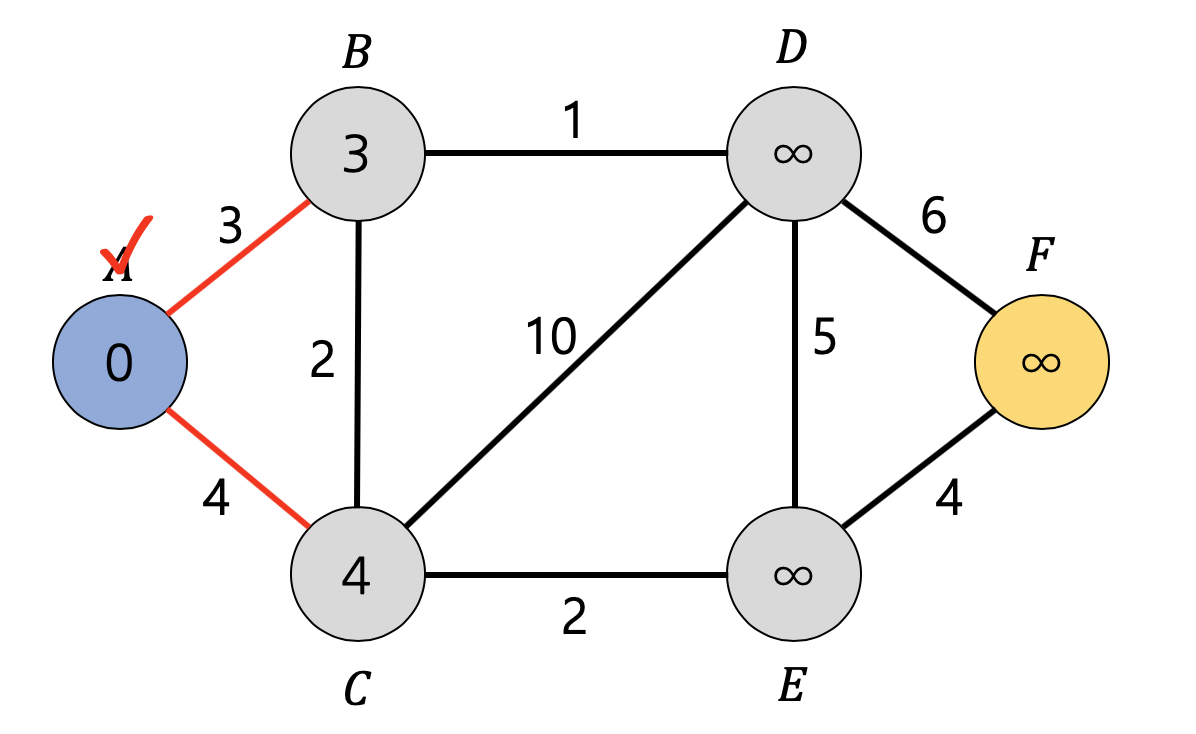
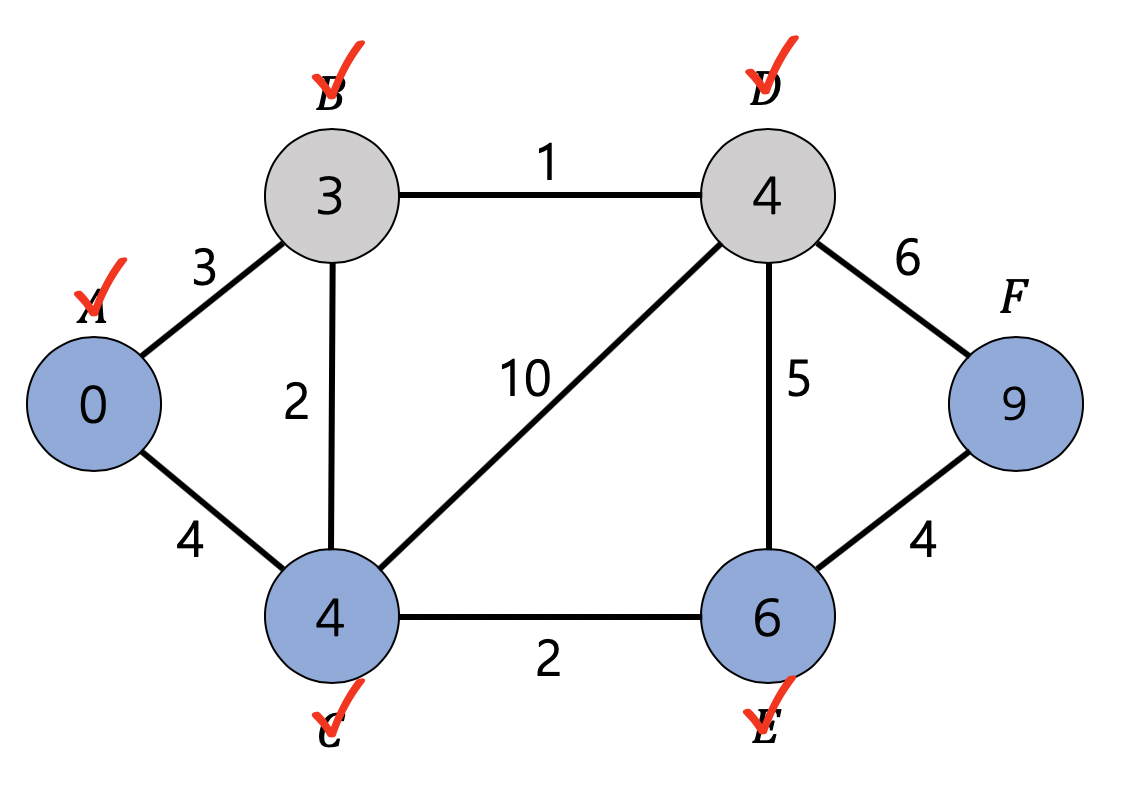
그 다음 노드에서도 마찬가지로 인접한 노드들의 edge를 확인하고 선택한다. 경로에 필요한 edge들의 합을 통해서 node를 업데이트 한다.

다익스트라 알고리즘은 방문하지 않은 노드가 없고, 목표 지점인 B까지 도달하면 멈추고, B까지 도달하는 최소의 weight인 path를 선택하게 된다.
Graph 코드는 Class로 구현해서 외우는 게 좋을 것 같습니다.
edges와 weights는 dictionary로 표현을 합니다. edges는 자신의 인접한 노드들을 표현하므로, list를 값으로 하여 연결된 노드들을 넣습니다. weights는 두 개의 노드 사이의 weight이므로 tuple(node, another_node)을 키(Key)로 하고, 가중치를 값(Value)로 합니다.
from collections import defaultdict
class Graph():
def __init__(self):
"""
self.edges is a dict of all possible next nodes
e.g. {'X': ['A', 'B', 'C', 'E'], ...}
self.weights has all the weights between two nodes,
with the two nodes as a tuple as the key
e.g. {('X', 'A'): 7, ('X', 'B'): 2, ...}
"""
self.edges = defaultdict(list)
self.weights = {}
def add_edge(self, from_node, to_node, weight):
# Note: assumes edges are bi-directional
self.edges[from_node].append(to_node)
self.weights[(from_node, to_node)] = weight
self.weights[(to_node, from_node)] = weight |
위의 그림을 예제로 edge 들을 추가합니다.
edges = [
('A', 'C', 4),
('A', 'B', 3),
('B', 'C', 2),
('B', 'D', 1),
('C', 'D', 10),
('C', 'E', 2),
('D', 'E', 5),
('D', 'F', 6),
('E', 'F', 3)
]
graph = Graph()
for edge in edges:
graph.add_edge(*edge) |
graph.edges와 graph.weights를 출력해보면 다음과 같습니다.
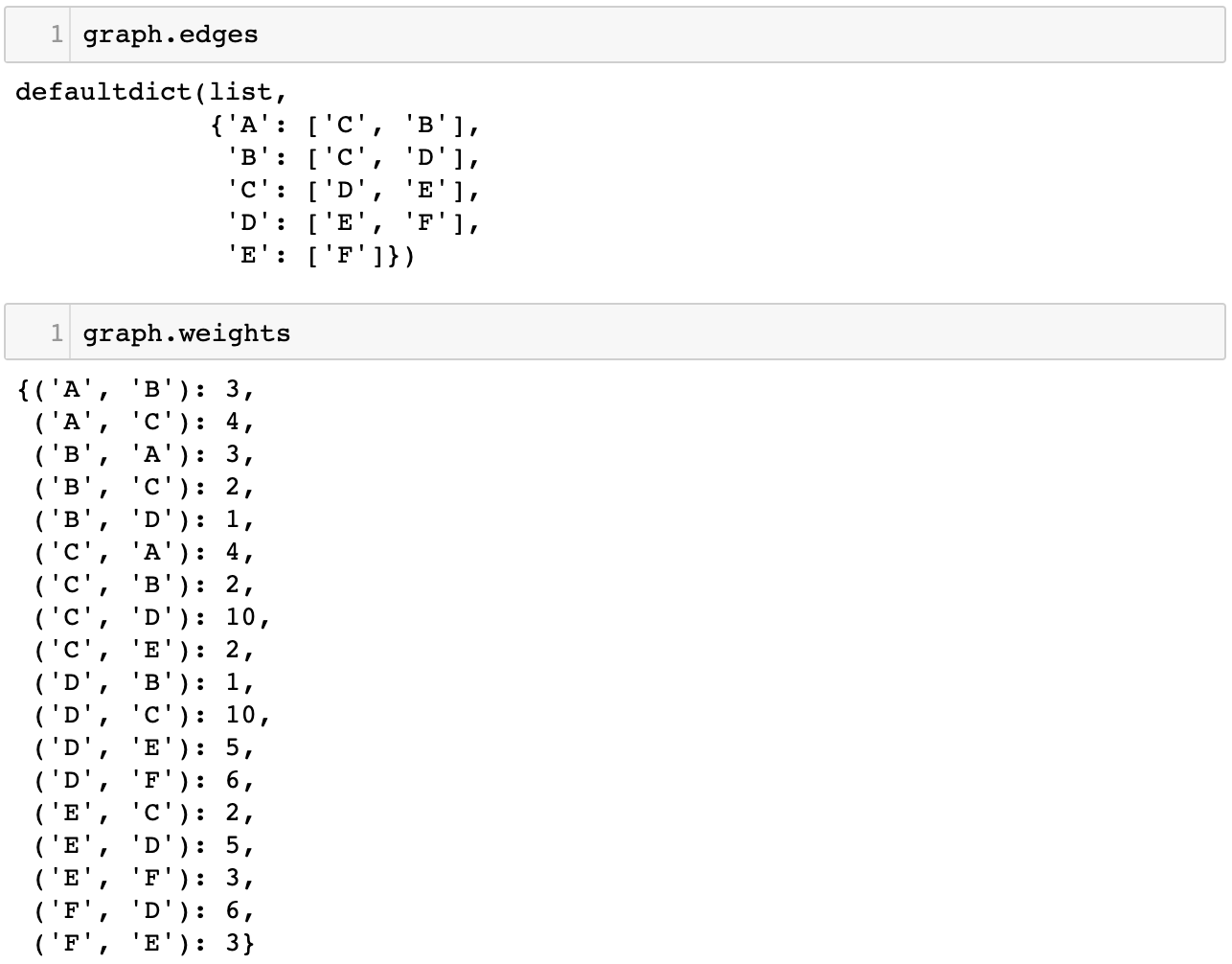
제일 중요한 것은 dijsktra 알고리즘 구현이겠죠?
def dijsktra(graph, initial, end):
# shortest paths is a dict of nodes
# whose value is a tuple of (previous node, weight)
shortest_paths = {initial: (None, 0)}
current_node = initial # 시작점 노드를 현재 노드로 추가한다.
visited = set() # 방문한 노드들을 추가한다.
while current_node != end:
visited.add(current_node) # 현재 노드를 방문한다.
destinations = graph.edges[current_node] # 인접한 노드를 살펴본다.
weight_to_current_node = shortest_paths[current_node][1] # 현재 방문 중인 노드의 weight
for next_node in destinations: # 인접한 노드 모두를 살펴본다.
# 현재 노드(current_node)와 인접한 노드(next_node)가 연결된 edge의 weight + 현재 weight
weight = graph.weights[(current_node, next_node)] + weight_to_current_node
if next_node not in shortest_paths: # shortest path에 없다면 현재를 추가한다.
shortest_paths[next_node] = (current_node, weight)
else: # 현재 shortest path에 있다면
current_shortest_weight = shortest_paths[next_node][1]
if current_shortest_weight > weight: # 현재 weight가 적다면 업데이트 한다.
shortest_paths[next_node] = (current_node, weight)
# 다음으로 이동할 node는 shortest path에서 아직 방문하지 않은 node로 이동한다.
next_destinations = {node: shortest_paths[node] for node in shortest_paths if node not in visited}
if not next_destinations:
return "Route Not Possible"
# weight가 가장 적은 노드로 이동한다.
current_node = min(next_destinations, key=lambda k: next_destinations[k][1])
destination_node = current_node # 현재 current_node는 destination node이다.
# destination에서 source로 이동하면서 node를 추가한다.
path = []
while destination_node is not None: # 시작 노드로 올 때 까지 반복한다.
path.append(destination_node)
next_node = shortest_paths[destination_node][0] # 다음 노드를 고른다.
print("next", next_node)
destination_node = next_node # destination_node를 다음 노드로 설정하면서
path = path[::-1] # 리스트를 반대로 정렬한다.
return path |
위의 그림대로 시작 노드를 A로 목표 지점 노드를 F로 하고 실행해보면 다음과 같습니다.
방문한 노드와 shortest_paths에서 노드와 weight가 업데이트 되는 것을 볼 수 있습니다.
